Hedging
Delta Hedging, Cumulative Delta and Hedging with Options
Today, we are going to talk about delta hedging.
The efficiency of hedging using options is dependent upon the delta of the options’ position mirroring the delta of the underlying position, in other words, creating a delta-neutral portfolio overall.
The delta of an option is a measure of the sensitivity of the option’s price to changes in the price of the underlying asset. It can be calculated by measuring the change in an option premium brought about by a small change in the price of the underlying.
Simplistically, delta (Δ) = change in option premium/change in price of underlying
A delta of 0 means that the premium is totally insensitive to small changes in the price of the asset. This will be the case for options that are far OTM.
A delta of 1 means that the premium will change by exactly the same monetary amount as the underlying. This will be the case for options that are deep ITM.
The sign of the delta enables us to distinguish between calls and puts.
Call deltas are positive – because the premium will rise when the price of the underlying rises.
Put deltas are negative – because the premium will fall when the price of the underlying rises.
Moneyness:
ATM = At The Money
ITM = It The Money
OTM = Out The Money
ABC inc share price = 575.
The 625 call has a delta of 0.30 and a premium of 26. The 525 put has a delta of –0.30 and a premium of 24.
If the share price rises to 585, using delta we can approximate the new call and put premiums: The share price has risen by 10.
The delta of the call is 0.30, so the change in premium will be 10 x 0.3 = 3 (ie, the call premium will rise from 26 to 29).
The delta of the put is –0.30, so the change in premium will be 10 x (–0.30) = –3 (ie, the put premium will fall from 24 to 21).
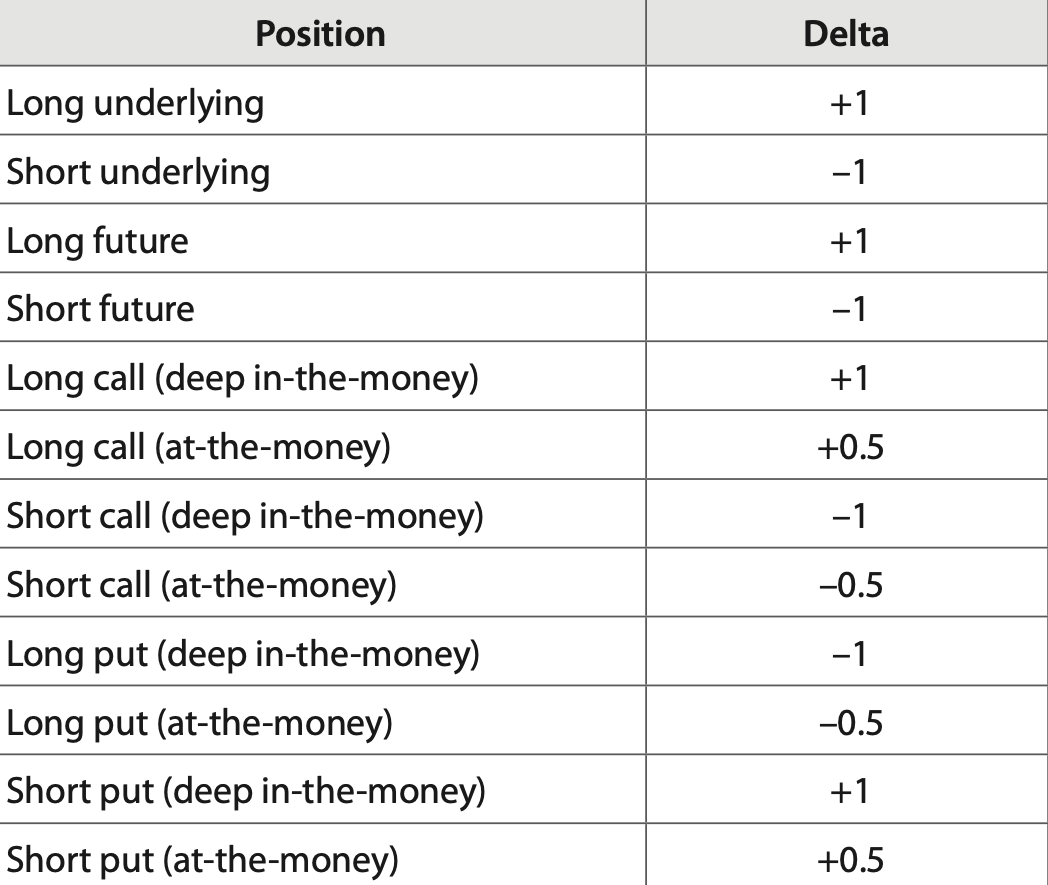
As seen, the delta for a deep ITM call option would be +1, and for a deep ITM put would be –1.
The delta for a far OTM call or put would be zero. Generally, an at-the-money option will have a delta of approximately 0.5, +0.5 for a call and –0.5 for a put.
Furthermore, the underlying physical asset and long futures will always have a delta of +1 and short futures will have a delta of –1.
As an OTM option approaches its expiration, its delta will approach zero. The longer to expiration, the slower the decline, but, as an option’s expiry date gets closer, the change in delta will increase.
The four most basic options positions (long call, short call, long put and short put) can be used to hedge against an underlying position.
Cumulative Delta
Deltas can also be used to measure the sensitivity of a portfolio containing futures/underlying, calls and puts. The delta calculated for a portfolio of positions is known as the cumulative delta.
In order to measure the cumulative delta of a combined portfolio, the deltas of the individual positions within it need to be added together. The cumulative delta then gives the overall sensitivity and direction of a portfolio. The directional bias is obtained by taking account of long and short positions (+ for long and – for short).
Cumulative deltas can be useful to gauge what is required to hedge a portfolio. A portfolio that has a cumulative delta of 0 is insensitive to price movements in the underlying asset – it is a hedged position, often referred to as delta neutral or delta hedged.
A long underlying position (delta +1) could be hedged by a short, deep in-the-money call (delta –1) to create a delta neutral portfolio (overall delta = +1 – 1 = 0). Alternatively, it could be hedged by two short at-the-money calls (–0.5 x 2 = –1), or a deep in-the-money long put (–1), or even two at-the-money long puts (–0.5 x 2 = –1).
Examples
Example 1
Investor A has written an ATM put.
The net delta position is (–1) x (–0.5) = +0.5
This is arrived at by taking the number of positions (1) and assigning a negative to it because it is a short position. This –1 is then multiplied by the delta of an ATM put of –0.5.
The result is that, if the price of the underlying rises by 10, Investor A’s position improves by 5. The price of the put would have decreased, thus showing a profit on the trade. A decrease in the underlying price would show a loss.
Example 2
Investor B is long five ITM calls with a delta of 0.7. Investor B’s net delta is (+5) x (+0.7) = +3.5
If the price of the underlying rises by 1, Investor B’s position improves by 3.5. The price of each of the calls would have gone up by 0.7 and he has five of them.
Example 3
Investor C has the following port on the same underlying:
Long 10 futures Net Delta [Net Δ] is (+10) x (+1) = +10
Short 3 OTM calls (delta of 0.30). Net Δ is (-3) x (+0.30) = -0.90
Long 4 ITM puts (delta -0.65). Net Δ is (+4) x (-0.65) = -2.60
Short 5 OTM puts (delta -0.15). Net Δ is (-5) x (-0.15) = +0.75
Long 8 deep OTM calls (delta 0). Net Δ is (+8) x (0) = 0
The Cumulative Delta is: +7.25 which is a very bullish position - equivalent to being long just over seven futures.
In order to delta hedge, positions with a cumulative delta of –7.25 need to be added, eg, sell seven futures and buy a put with a delta of 0.25.
It is also useful to note that such delta hedging only hedges against price risk; other risks associated with time decay, volatility and basis still remain. Delta is also a dynamic measure so, as time passes, or the price of the underlying asset changes, the delta will change.
The Other Greeks
In addition to delta, there are several other greek measures for calculating the relationship between an option’s price and changes in the price of the underlying asset, as well as over time.
Gamma γ
Gamma is the measure of how delta changes (the rate of change of delta) with respect to movements in the price of the underlying. It is small when the option is either deep in-the-money, or far out-of-the- money. It is at its greatest when the option is ATM, especially when the option is close to expiry.
Traders will monitor the impact of gamma on the premiums of options. Short-dated ATM options are more volatile than longer-dated ones, and these differences may present an opportunity for trading profits. Asset managers also use gamma in their dynamic hedging strategies. As indicated, a portfolio can be delta neutral. The delta would have to be monitored and perhaps re-balanced because of the impact of gamma on the portfolio delta.
Since gamma is the measure of changes in delta, it represents the required adjustments to any hedges associated with a single option’s position or a portfolio of options. It represents the size of these adjustments.
For option holders, the changes in gamma usually correspond to profitable trades, ie, the required adjustments to the delta hedge of the underlying asset will result in a profit. For example, if an investor has a long position on a call option on an individual share, as the share’s price rises the option’s delta will increase, as measured by gamma, and the investor will sell the adjustment or change to delta at a higher price. Therefore, when one has a long position on an option or a net long position in an option portfolio, one is said to have a positive gamma indicator or simply positive gamma. The opposite is true when one is an option writer or holds a net short option portfolio.
When gamma is positive, any adjustments in the portfolio to bring it back to delta neutral requires buying low and selling high (ie, profitable adjustments). When gamma is negative, any such adjustments are the opposite, ie, loss-making.
Vega ν
Vega is a measure of how a 1% change in implied volatility affects an option’s price. Vega is always positive for long options positions – both calls and puts. It is greatest for ATM options. The further an option goes ITM or OTM, the smaller vega will become. Time increases the effect of changes in volatility upon an option’s value. Therefore, vega is higher for long-dated options than short-dated options and falls as an option approaches its expiration date. Vega can change even if there is no dramatic change in the movements of the underlying asset’s price; it is affected by any change in expected volatility.
Vega is useful since it measures an option’s or option portfolio’s sensitivity to both market sentiment (expected volatility) and current market conditions. Many traders/investors use vega as the key measure of profitability of their option positions since if they are delta neutral they are trading on an asset’s volatility and not on a specific direction, therefore vega tells them how well their positions are performing relative to current market conditions.
Theta θ
Theta is the measure of the rate of decline of an option’s value due to the passage of time. Theta represents how much an option’s value will change as one day passes and its underlying asset’s price remains steady. Theta can also represent the time decay on the value of an option. If all other factors are held constant, then an option will lose value as time moves closer to its maturity.
The measure of theta quantifies the risk that time imposes on options since they have an expiration date and in most cases are only exercisable for a certain period of time. Time has importance for option traders on a conceptual level more than a practical one.
Theta and Option Positions
Long calls and long puts always have negative theta.
Short calls and short puts always have positive theta.
Theta is highest for ATM options and gradually decreases as an option moves further ITM or OTM.
Theta (time decay) would increase sharply as an option approaches its expiration and can severely undermine a long option holder’s position, particularly if volatility is also decreasing at the same time. This is because theta is higher when either volatility is lower or there are fewer days to expiration.
Theta is used as a factor in combination with gamma and vega in determining trading strategies since it represents the change in an option’s fair value per day. As a percentage of the decay in an option’s value, theta increases as expiration gets closer. Therefore, if vega is falling a trader is more likely to sell an option that is a few days from expiration rather than one that is six months away.
Remember that the efficiency of hedging using options is dependent upon the delta of the options’ position mirroring the delta of the underlying position, in other words, creating a delta-neutral portfolio overall.
Question
You have the following position in the same underlying asset:
Short four futures, Short three ATM calls, Long six deep ITM puts
What is your cumulative delta? How could you delta hedge?
Answer question in comments or if you are shy by Twitter DM.
Any questions. Please reach out.
For the next post, would you like me write about how to hedge/delta hedge with futures or talk about synthetics and option strategies (the construction + motivations for trading them)?
P.S. A long term stock I like here - CLVT - Clarivate PLC.
Thanks,
LF



I got-11.5 Cumulative Delta and Hedged it with 5 Long underlying, 5 long call deep ITM, 1 short put deep ITM, 1 long call ATM? I get the principle of it I think, but guess there are better combinations to be had when hedging?!
I'm giving this a try : in your example I get a Delta of -11.5.
To Delta hedge : buy 11 ATM calls, and buy 6 futures.
I don't know if my Delta hedge makes any sense or not.
Just trying to get a feel for this !
I would like to hear more about futures and hedge/Delta hedging.